题目来源
灵感来自于《算法图解》第 7 章 「狄克斯特拉算法」,图片和代码也是来自该书。
题目描述
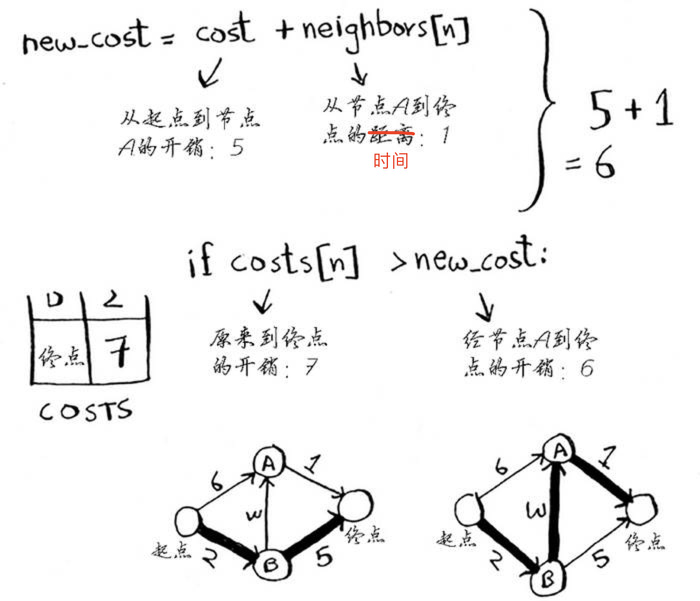
假设你住起点,公司在终点。坐地铁上班路线有三条,起点 -> A -> 终点;起点 -> B -> A -> 终点;起点 -> B -> 终点。请用狄克斯特拉算法,计算出早上坐地铁上班,最短用时多久就能到公司(不算换乘时间)?2 代表 20 分钟。路线图如下:
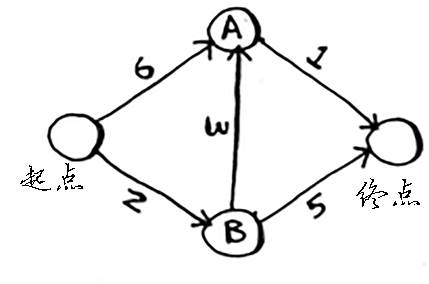
提示:可用三个散列表来表示各节点之间的关系:

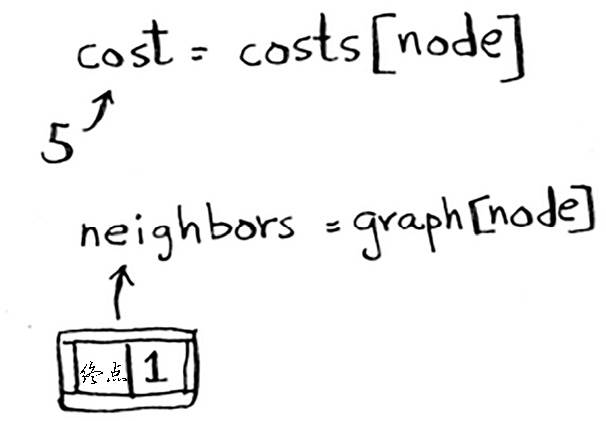
- GRAPH 表:记录所有节点到相邻节点(邻居)的时间
- COSTS 表:记录起点到其他节点的时间(开销)
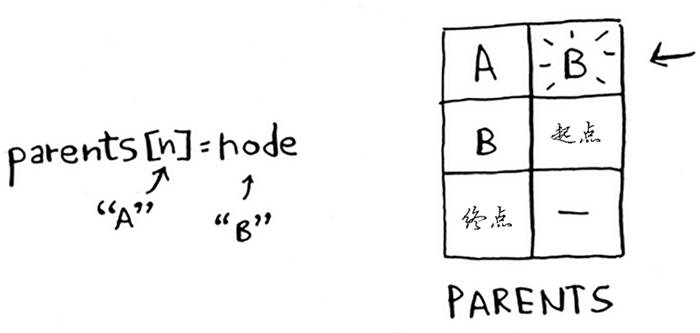
- PARENTS 表:记录除起点以外的所有节点和其父节点(终点的父节点不确定)
解题方案
思路
- 标签:
狄克斯特拉算法、哈希表 - 狄克斯特拉算法:用于计算单源最短路径的算法
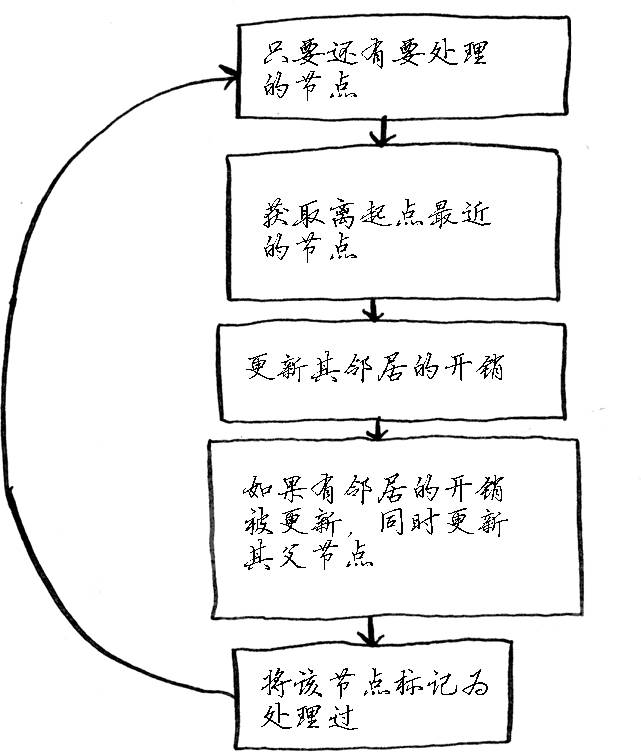
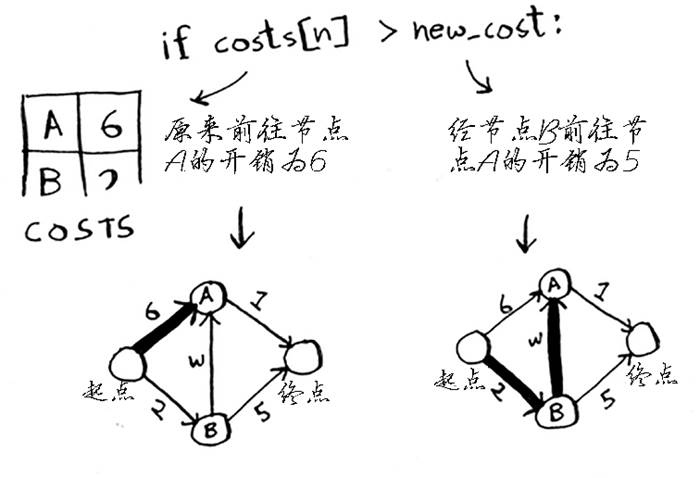
- 从 COSTS 表中找出离起点用时最短(开销最低)的相邻节点(B)
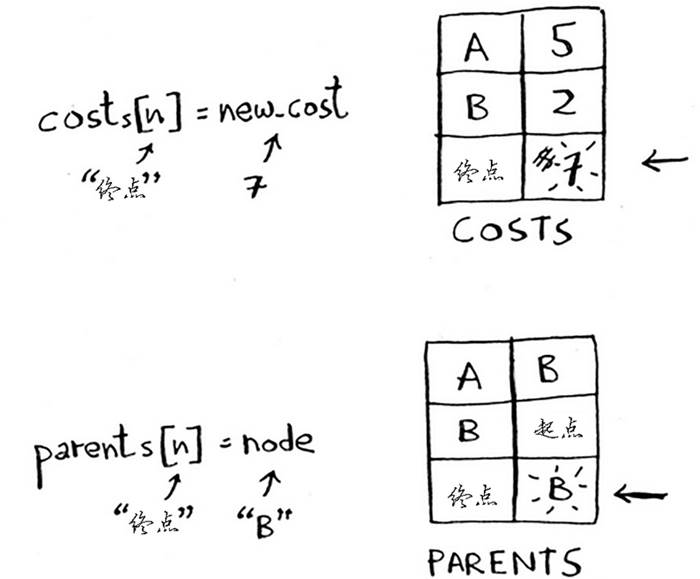
- 遍历 B 节点的邻居,如果起点经 B 到邻居的开销更低,更新 COSTS 表中此邻居的开销
- 同时更新 PARENTS 表此邻居的父节点
- 遍历完所有邻居后,将节点标记为已处理过
- 继续从 COSTS 表中找出未被处理过的、离起点开销最低的节点,循环,直到所有节点都被处理过
- 最终 COSTS 表中终点对应的值,就是结果
- 时间复杂度:O (n^2^) (n 节点) * (n 邻居)
代码
# Python3 |
图解

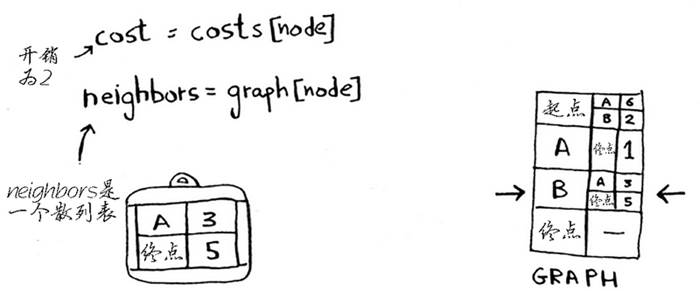
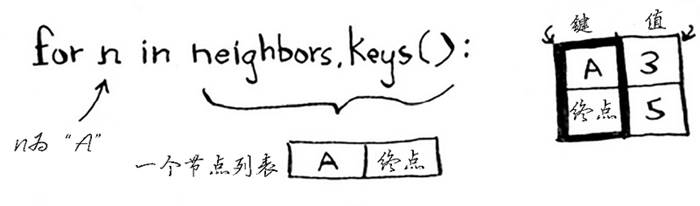


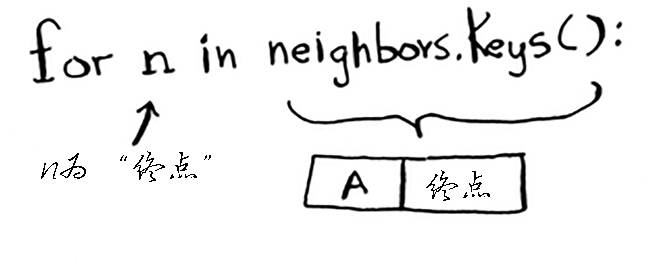






思考
如果要问:「早上地铁坐那条路线耗时最短?」应该怎样修改代码?
