浅析七种经典排序算法

发表于 | 更新于 | | 阅读次数

本文分析冒泡、快速、选择、插入、希尔、归并和堆排序，为了对以下各个算法进行方便的测试，测试主方法体如下（Java 实现）：

public class Sort {
   public static void main(String[] args) {
        int[] input = {5, 4, 7, 1, 6, 2, 8, 9, 10};
        // 此处调用方法，以调用冒泡排序为例
        bubbleSort(input);
        for (int i = 1; i <= input.length; i++) {
            System.out.println(input[i - 1]);
        }
    }
}

本篇博文所有排序实现均默认 从小到大。

冒泡排序（Bubble Sort）

每一次通过两两比较找到最大（小）的元素放在未排序序列的最后，直至有序。

步骤

  1. 比较两个相邻的元素。如果前面比后面个大（小），就交换顺序。
  2. 从第 1 个数与第 2 个数开始比较，直到第 n-1 个数与第 n 个数结束。到最后，最大（小）的数就 “ 浮 “ 在了最上面。
  3. 持续每次对前面越来越少的未排序元素重复上面的步骤，直到所有元素有序。

排序演示

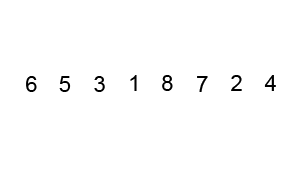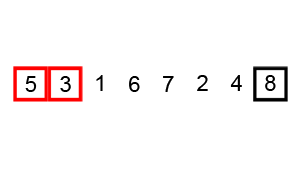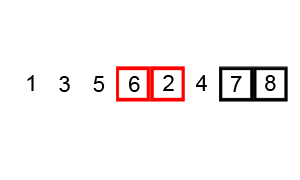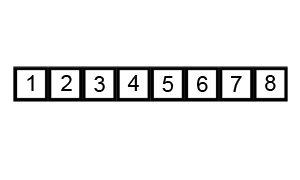
image

源代码（Java 实现）

public static void bubbleSort(int[] input) {
        for (int i = 1; i <= input.length; i++) {
            for (int j = 1; j <= input.length - i; j++) {
                if (input[j - 1] > input[j]) {
                    int temp = input[j - 1];
                    input[j - 1] = input[j];
                    input[j] = temp;
                }
            }
        }
}

算法指标分析

最好时间复杂度：O(n^2)。当元素有序时，要比较。n 个元素，每个元素比较 n次。

最坏时间复杂度：O(n^2)。当元素无序时，也要比较。

平均时间复杂度：O(n^2)。

辅助空间：不需要额临时的存储空间来运行算法，所以为 O(1)。

稳定性：因为排序方式是相邻数比较后交换，如果序列中有相等的两个数，待两数相邻时，不会交换两者的位置，所以稳定。

冒泡排序的两种优化方式

优化 1：

某一趟遍历如果没有元素交换，flag 标记依旧为 true。说明已经排好序了，结束迭代。

public static void bubbleSort2(int[] input) {
        for (int i = 1; i <= input.length; i++) {
            boolean flag = true;
            for (int j = 1; j <= input.length - i; j++) {
                if (input[j - 1] >  input[j]) {
                    int temp = input[j - 1];
                    input[j - 1] = input[j];
                    input[j] = temp;
                }
                flag = false;
            }
            if (flag)
                break;
        }
}

算法指标分析

最好时间复杂度：当序列有序时。第一个 for 循环中，第 2/3/11/12 行语句执行 1 次，即频度为 1；第二个 for 循环中，第 4、5、9 行语句执行 n-1 次，即频度为 n-1。T(n) = 3*(n-1)+4 = 3n+1 = O(n)。所以最好时间复杂度为 O(n)。

最坏时间复杂度：当序列为逆序时。第一个 for 循环的频度为 n；第二个 for 循环中，j 可以取 1,2,…,n-1，所以第 3/4/6/7/8 语句，频度均为 (1+n-1)✖️(n-1)/2。T(n) = n✖️(n-1)/2+n = O(n^2)。所以最坏时间复杂度为 O(n^2)。

我们可以看出在嵌套层数多的循环语句中，由最内层语句的频度 f(n) 决定时间复杂度。

优化 2：

记录某次遍历时最后发生元素交换的位置（LastExchange），这个位置之后的数据显然已经有序，不用再排序了。因此通过记录最后发生元素交换的位置就可以确定下次循环的范围。

public static void bubbleSort3(int[] input) {
        int LastExchange = input.length;
        boolean flag = true;
        for (int i = 1; i <= input.length; i++) {
            int k = LastExchange;
            for (int j = 1; j <= k - 1; j++) {
                if (input[j - 1] > input[j]) {
                    int temp = input[j - 1];
                    input[j - 1] = input[j];
                    input[j] = temp;
                }
                LastExchange = j;
                flag = false;
            }
            if (flag)
                break;
        }
}

快速排序（Quick Sort）

又称划分交换排序（partition-exchange sort）。采用了分而治之的思想。

思路

  1. 递归结束条件：1 个数或 0 个数不用排序
  2. 找一个基准值，从两边向中间遍历，将左边大于基准值与右边小于基准值交换。一次排序后，左边所有的数比右边所有的数小

选择末尾数为基准值

  • 如果选择中位数作为基准值，考虑条件太多，比如 20, 2, 10 ,1, 6, 9

排序演示

6  5  3  1  8  7  2  4
↑                 ↑  ^
2  5  3  1  8  7  6  4
   ↑     ↑           ^
2  1  3  5  8  7  6  4
         ↑           ^
2  1  3 [4] 8  7  6  5

源代码

// Java
public static void quickSort(int[] input) {
        quick_sort(input, 0, input.length - 1);
}

private static void quick_sort(int[] input, int start, int end) {
        if (start >= end) {
            return;
        }
        int left = start, right = end - 1;
        int pivot = input[end];
        while (left < right) {
            // 跳过
            while (input[left] <= pivot && left < right) {
                left++;
            }
            while (input[right] >= pivot && left < right) {
                right--;
            }
            int temp = input[left];
            input[left] = input[right];
            input[right] = temp;
        }
        // 此时左右指针重合（left == right），其指向元素可能大于基准值
        if (input[left] >= pivot) {
            int temp = input[left];
            input[left] = pivot;
            input[end] = temp;
        } else
            left++; // 跳过已经有序的中数
        quick_sort(input, start, left - 1);
        quick_sort(input, left, end);
}

算法指标分析

最好时间复杂度：n*log n。n：交换；log n：调用栈的高度（2^(high-1) = n），数组有序且基准值每次都是中间值。

最坏时间复杂度：n^2。调用栈的高度为 n，基准值每次都是最值。

平均时间复杂度：O(n log n)。随机选择基准值 (log n + n)/2 = log n

辅助空间：需要额临时的存储空间来运行算法，所以为 O(n log n)~O(n)。

稳定性：不稳定。

更多实现方式：快速排序的几种实现方式

选择排序（Selection Sort）

每一次通过选择找到未排序序列的最小（大）元素放在已排序序列的末尾（交换位置），直至有序。

思路

  • 选择排序一遍遍历，只交换一次，而冒泡排序会交换多次。

步骤

  1. 未排序序列中找到最小（大）元素，存放到序列的起始位置。
  2. 再从剩余未排序元素中继续找到最小（大）元素，放到已排序序列的末尾。
  3. 以此类推，直到所有元素均排序完毕。

排序演示

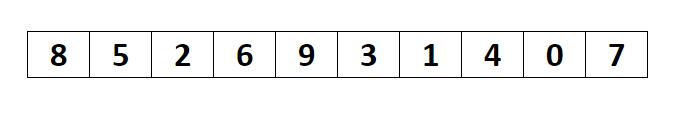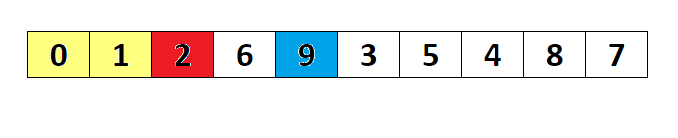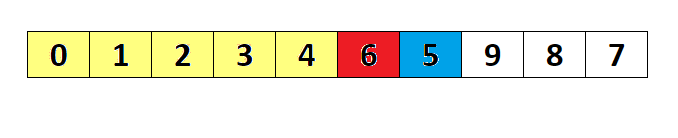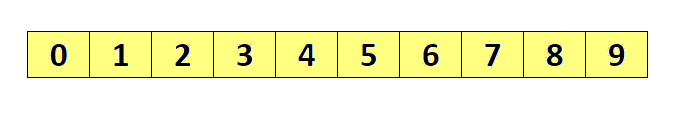
image

源代码（Java 实现）

public static void selectionSort(int[] input) {
        for (int i = 1; i <= input.length; i++) {
            int minIndex = i - 1;
            for (int j = i; j < input.length; j++) {
                if (input[minIndex] > input[j])
                    minIndex = j;
            }
            if (minIndex != i - 1) {
                int temp = input[minIndex];
                input[minIndex] = input[i - 1];
                input[i - 1] = temp;
            }
        }
}

算法指标分析

不管序列有序还是逆序，第二个 for 循环的频度为 n*(n-1)/2。所以最坏时间复杂度和最好时间复杂度均为 O(n^2)。

平均时间复杂度：O(n^2)

辅助空间：不需要额临时的存储空间来运行算法，所以为 O(1)。

稳定性：不稳定。举例，5、7、5、2、9，找到最小 2 时，2 与 5 交换，此时两个 5 的相对位置发生改变。

插入排序（Insertion Sort）

对于每个未排序元素，在已排序序列中从后向前扫描，找到相应位置并插入。

思路

  • 插入时，需要移动后面的元素？插入并不是真正的插入，而是从后往前两两交换，最终效果像插入一样。

步骤

  1. 第 1 个元素视为已经被排序
  2. 取未排序的第 1 个元素，在已排序序列中从后向前扫描
  3. 如果被扫描的元素大于新元素，将该元素后移一位
  4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤 2~5
  7. 如果全部有序，结束迭代

排序演示

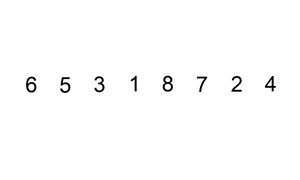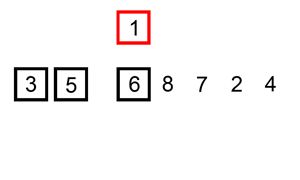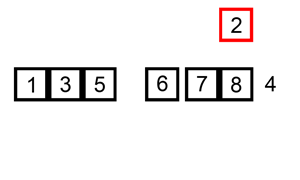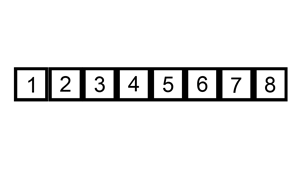
image

6 5 3 1 8 7 2 4
5 6 3 1 8 7 2 4   5 6 交换
5 3 6 1 8 7 2 4   6 3 交换
3 5 6 1 8 7 2 4   3 5 交换

源代码 (Java 实现)

public static void insertionSort(int[] input) {
        for (int i = 1; i < input.length; i++) {
            for (int j = i; j > 0; j--) {
                if (input[j] < input[j - 1]) {
                    int temp = input[j];
                    input[j] = input[j - 1];
                    input[j - 1] = temp;
                }
                else break;
            }
        }
}

算法指标分析

最好时间复杂度：当序列有序时。当第一个 for 循环运行时，在第二个 for 循环中，因为序列有序，所以只会相邻比较 1 次，就跳出循环。所以两个循环的频度均为 n-1，所以最好时间复杂度均为 O(n)。

最坏时间复杂度：当序列逆序时。第二个 for 循环的频度为 n(n-1)/2。所以最坏时间复杂度均为 O(n^2)。

平均时间复杂度：O((n+n^2)/2) = O(n^2)。

辅助空间：不需要额临时的存储空间来运行算法，所以为 O(1)。

稳定性：因为排序方式是两两比较，序列中如果相邻两个数相等，不会交换两者的位置，所以稳定。

希尔排序（Shell Sort）

希尔排序，也称递减增量排序算法，实质上是一种分组插入排序算法。是插入排序的一种更高效的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：

  • 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
  • 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

步骤

  1. 假设数组为 {5, 4, 7, 1, 6, 2, 8, 9, 10}，如果我们以步长为 4 开始进行排序，我们可以通过将这列表放在有 4 列的表中来更好地描述算法，这样他们就应该看起来是这样：

    5, 4, 7, 1
    6, 2, 8, 9
    10

  2. 将数组列在一个表中并对列分别进行插入排序

    5, 2, 7, 1
    6, 4, 8, 9
    10

  3. 重复这过程，不过每次用更长的列（步长更小，列数更少）来进行，如下步长为 2。

    5, 2
    7, 1
    6, 4
    8, 9
    10

  4. 最后整个表就只有一列了（ 再进行插入排序）

    5, 1, 6, 2, 7, 4, 8, 9, 10

源代码（Java 实现）

public static void shellSort(int[] input) {
        int len = input.length, j;
        int gap = Math.round(len / 2);
        for (; gap > 0; gap /= 2) // 步长每次就减少一倍
            for (int i = gap; i < len; i++) {
                int temp = input[i];
                for (j = i - gap; j >= 0 && temp < input[j]; j -= gap) {// 列排序
                    input[j + gap] = input[j];
                    input[j] = temp;
                }
            }
}

算法指标分析

最好时间复杂度：当序列有序时。最好时间复杂度均为 O(n^s)，1<s<2，跟算法步长有关。

最坏时间复杂度：当序列逆序时。最坏时间复杂度均为 O(n^2)。

平均时间复杂度：O(n log n)~O(n^2)。

辅助空间：不需要额临时的存储空间来运行算法，所以为 O(1)。

稳定性：不稳定。解释如下：

假设，序列为 5,5,7,3,2，取步长为 3 分组为
5,5,7
3,6
3 和 5 交换位置后，两个 5 的相对顺序发生改变，所以不稳定

堆排序（HeapSort）

使用到二叉堆这种数据结构，二叉堆是平衡二叉树。它具有以下性质：

  1. 父节点的值大于等于左右节点的值，为最大堆（大顶堆）；父节点的值小于于等于左右节点的值，为最小堆（大顶堆）
  2. 每个父节点的左右节点都是二叉堆（大顶堆或小顶堆）

本质上堆排序是由数组实现。

步骤

  1. 调用构造大顶堆方法，将数组构造成大顶堆。叶子节点相当于大顶堆，假设数组下标范围为 0~n-1，则从下标 n/2 开始的元素（叶子节点）均为大顶堆。所以从下标 n/2-1 开始的元素（父节点）开始，向前依次（下标减 1）构造大顶堆。
  2. 堆排序：由于堆是用数组模拟的。构造的大顶堆相当于在数组中无序。因此需要将数组有序化。思想是循环将根节点与最后一个未排序元素交换，再调用构造大顶堆方法。循环结束后，整个数组就是有序的了。
  3. 构造大顶堆方法：调整节点，使得左右子节点小于父节点，保证根节点是当前堆中最大的元素。

    排序演示：

    第一次将数组构造成大顶堆时，跟此演示稍有不同，默认按数组顺序放入二叉堆，没有边放边构造。

image

源代码（Java 实现）

public static void heapSort(int[] input) {
        int i = input.length/ 2 - 1;// 最后一个非叶子节点
        // 将数组构造成大顶堆
        for (; i >= 0; i--)
            maxHeapify(input, i, input.length - 1);
        // 堆排，将大顶堆转换成有序数组
        for (i = input.length - 1; i >= 0; i--) {
            int temp = input[0];
            input[0] = input[i];
            input[i] = temp;
            maxHeapify(input, 0, i - 1);
        }
}
// 构造大顶堆
public static void maxHeapify(int[] input, int start, int end) {
        int child;
        int root = start;
        // 父节点不是叶子节点时循环；只有一个根节点时不再比较
        for (; root <= (end - 1) / 2 && end > 0; ) {
            child = root * 2 + 1;// 调整子节点
            // 取较大的子节点
            if (child + 1 <= end && input[child] < input[child + 1])
                child += 1;

            if (input[root] < input[child]) {
                // 交换较小父节点和较大子节点的位置
                int temp = input[root];
                input[root] = input[child];
                input[child] = temp;
                root = child;// 较大的子节点成为父节点
            } else
                break;
        }
}

算法指标分析

最好时间复杂度：当序列有序时。最好时间复杂度均为 O(n log n)，跟算法步长有关。

最坏时间复杂度：当序列逆序时。最坏时间复杂度均为 O(n log n)。

平均时间复杂度：O(n log n)。

辅助空间：不需要额临时的存储空间来运行算法，所以为 O(1)。

稳定性：不稳定。

二分归并排序（MergeSort）

先递归分解序列，再合并序列。也采用了分治法的思想。

步骤

  1. 合并：合并的条件是两个序列都有序，当序列中只有 1 个元素时我们认为也是有序的；合并的方法是通过比较将较小元素先放入临时数组，再将左、右序列剩余元素放入。
  2. 分解：先将源序列从中位数（中数）分开为左右序列，递归分解左序列，中数不断减小，直到为 1。此时左、右序列中只有一个元素，通过比较将左、右序列合并为左序列后，再递归分解右序列（也分解到只有一个元素）。

    排序演示

    此图主要思想一致，但代码实现过程中，6531 合并完成时，8724 还没分解。

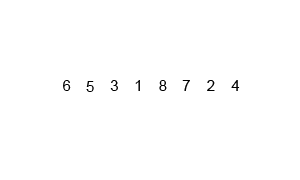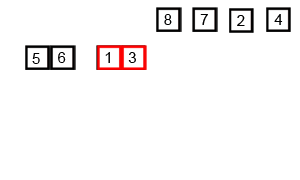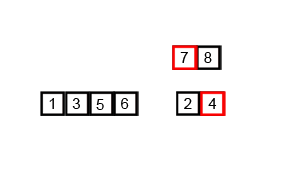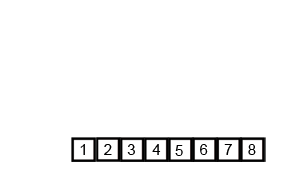
image

源代码（Java 实现）

public static void mergeSort(int[] input) {
        merge_sort(input, 0, input.length - 1);
    }
public static void merge_sort(int[] input, int start, int end) {
        int middle;
        // 当序列中只有一个元素时，结束当前递归
        if (start < end) {
            middle = (start + end) / 2;// 找出中位数（中数），中数越来越小
            merge_sort(input, start, middle);// 中数左侧序列二分
            merge_sort(input, middle + 1, end);// 中数右侧序列二分
            merge(input, start, middle, end);// 合并成源序列
        }
}
// 合并成源序列
public static void merge(int[] input, int left, int middle, int right) {
        int[] temp = new int[right - left + 1];// 用于存放新排好序的序列
        int i = left;// 左序列的起始下标
        int j = middle + 1;// 右序列的起始下标
        int n = 0;//temp[] 数组的起始下标
        // 通过比较将较小元素先放入 temp 数组
        while (i <= middle && j <= right) {
            if (input[i] < input[j]) {
                temp[n] = input[i];
                i++;
            } else {
                temp[n] = input[j];
                j++;
            }
            n++;
        }
        // 将第一个序列的剩余元素放入 temp[]
        while (i <= middle) {
            temp[n] = input[i];
            i++;
            n++;
        }
        // 将第二个序列的剩余元素放入 temp[]
        while (j <= right) {
            temp[n] = input[j];
            j++;
            n++;
        }
        // 将 num[] 中的元素复制到数组 input
        for (int x = 0, y = left; x <= n && y <= right; x++, y++)
            input[y] = temp[x];
}

算法指标分析

最好时间复杂度：当序列有序时。最好时间复杂度均为 O(n log n)。

最坏时间复杂度：当序列逆序时。最坏时间复杂度均为 O(n log n)。

平均时间复杂度：O(n log n)。

辅助空间：需要新建额外临时的存储空间来存储新排好序的序列，每一次归并都需要重新新建，新建频度为 n，所以辅助空间为 O(n)。

稳定性：稳定。因为两两比较。

时间复杂度

时间频度：一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为 T(n)。

时间复杂度：在刚才提到的时间频度中，n 称为问题的规模，当 n 不断变化时，时间频度 T(n) 也会不断变化。但有时我们想知道它变化时呈现什么规律。为此，我们引入时间复杂度概念。 一般情况下，算法中基本操作重复执行的次数是问题规模 n 的某个函数，用 T(n) 表示，若有某个辅助函数 f(n), 使得当 n 趋近于无穷大时，T(n)/f(n) 的极限值为不等于零的常数 C，则称 f(n) 是 T(n) 的同数量级函数。记作 T(n)=O(f(n)), 称 O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

虽然对 f(n) 没有规定，但是一般都是取尽可能简单的函数。例如，O(2n^2+n+1) = O(3n^2+n+3) = O(7n^2 + n) = O(n^2) ，一般都只用 O(n^2) 表示就可以了。注意到大 O 符号里隐藏着一个常数 C，所以 f(n) 里一般不加系数。如果把 T(n) 当做一棵树，那么 O(f(n)) 所表达的就是树干，只关心其中的主干，其他的细枝末节全都抛弃不管。

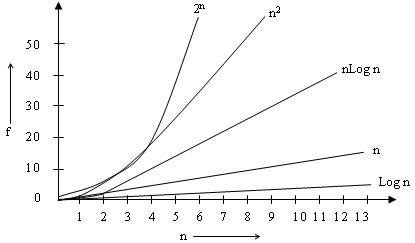
image

由上图可见，常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log n)＜Ο(n)＜Ο(nlog n)＜Ο(n^2)＜Ο(n^3)＜…＜Ο(2^n)＜Ο(n!)。

分析以下代码的时间复杂度。

i=1;     
while (i<=n)  
  i=i*2;

第 1 行语句的频度为 1
设第 3 行语句的时间频度为 f(n)k，2f(n) = n; –>f(n) = log n
第 2 行语句跟第 2 三行的频度一样，为 log n
以上代码的 T(n) = 2log n+1 = O(log n)

由此可见，T(n) 由最大的 f(n) 决定。在嵌套层数多的循环语句中，由最内层语句的频度 f(n) 决定 T(n)。
注：log n = log₂n = lg n；复杂度中以 2 为底，不是数学中以 10 为底。

空间复杂度

一个算法的空间复杂度 (Space Complexity) 定义为该算法所耗费的存储空间，它也是问题规模 n 的函数。渐近空间复杂度也常常简称为空间复杂度。

一个算法在计算机存储器上所占用的存储空间，包括：

  • 存储算法本身所占用的存储空间
  • 算法的输入输出数据所占用的存储空间
  • 算法在运行过程中临时占用的存储空间

我们将算法在运行过程中临时占用的存储空间称为辅助空间，它随算法的不同而异，另外两种存储空间与算法本身无关。

如当一个算法的空间复杂度为一个常量，即不随被处理数据量 n 的大小而改变时，辅助空间可表示为 O(1)；当一个算法的空间复杂度与以 2 为底的 n 的对数成正比时，辅助空间可表示为 O(1og₂n)；当一个算法的空间复杂度与 n 成线性比例关系时，辅助空间可表示为 O(n)。

稳定性

在排序过程中，具有相同数值的对象的相对顺序被不被打乱。如果可以保证不被打乱就是稳定的，如果不能保证就是不稳定的。

总结

根据每个排序算法关于稳定性的指标分析，可以得出以下结论：

  1. 如果每次变换都只是交换相邻的两个元素，那么就是稳定的。
  2. 如果每次都有某个元素和比较远的元素的交换操作，那么就是不稳定的。

以上算法博主亲测都能正确运行。以下是上述七种算法的性能指标分析对比情况。

排序方式 平均时间复杂度 最好时间复杂度 最坏时间复杂度 空间复杂度
（辅助空间）		 稳定性
冒泡排序 O(n^2) O(n^2) O(n^2) O(1) 稳定
快速排序 O(n log n) O(n log n) O(n^2) O(log n)~O(n) 不稳定
选择排序 O(n^2) O(n^2) O(n^2) O(1) 不稳定
插入排序 O(n^2) O(n) O(n^2) O(1) 稳定
希尔排序 O(n log n)~O(n^2) O(n^s)
（0<s<1，跟步长有关）		 O(n^2) O(1) 不稳定
堆排序 O(n log n) O(n log n) O(n log n) O(1) 不稳定
二分归并排序 O(n log n) O(n log n) O(n log n) O(n) 稳定

参考资料

deppwang wechat

评论默认使用 ，你也可以切换到 来留言。